A kind anonymous patron offers this prompt, which I totally fucked up getting done in July:

Something to do with programming languages? Alternatively, interesting game mechanics!

It’s been a while since I’ve written a thing about programming languages, eh? But I feel like I’ve run low on interesting things to say about them. And I just did that level design article, which already touched on some interesting game mechanics… oh dear.

Okay, how about this. It’s something I’ve been neck-deep in for quite some time, and most of the knowledge is squirrelled away in obscure wikis and ancient forum threads: getting data out of Pokémon games. I think that preserves the spirit of your two options, since it’s sort of nestled in a dark corner between how programming languages work and how game mechanics are implemented.

A few disclaimers

In the grand scheme of things, I don’t know all that much about this. I know more than people who’ve never looked into it at all, which I suppose is most people — but there are also people who basically do this stuff full-time, and that experience is crucial since so much of this work comes down to noticing patterns. While it sure helped to have a technical background, I wouldn’t have gotten anywhere at all if I weren’t acquainted with a few people who actually know what they’re doing. Most of what I’ve done is take their work and run with it.

Also, I am not a lawyer and cannot comment on any legal questions here. Is it okay to download ROMs of games you own? Is it okay to dump ROMs yourself if you have the hardware? Does this count as reverse engineering, and do the DMCA protections apply? I have no idea. But that said, it’s not exactly hard to find ROM hacking communities, and there’s no way Nintendo isn’t aware of them (or of the fact that every single Pokémon fansite gets their info from ROMs), so I suspect Nintendo simply doesn’t care unless something risks going mainstream — and thus putting a tangible dent in the market for their own franchise.

Still, I don’t want to direct an angry legal laser at anyone, so I’m going to be a bit selective about what resources I link to and what I merely allude to the existence of.

Some basics

This is, necessarily, a pretty technical topic. It starts out in binary data and spirals down into microscopic details that even most programmers don’t need to care about. Sometimes people approach me to ask how they can help with this work, and all I can do is imagine the entire contents of this post and shrug helplessly.

Still, as usual, I’ll do my best to make this accessible without also making it a 500-page introduction to all of computing. Here is some helpful background stuff that would be clumsy to cram into the rest of the post.

Computers deal in bytes. Pop culture likes to depict computers as working in binary (individual bits or “binary digits”), which is technically true down on the level of the circuitry, but virtually none of the actual logic in a computer cares about individual bits. In fact, computers can’t access individual bits directly; they can only fetch bytes, then extract bits from those bytes as a separate step.

A byte is made of eight bits, which gives it 2⁸ or 256 possible values. It’s helpful to see what a byte is, but writing them in decimal is a bit clumsy, and writing them in binary is impossible to read. A clever compromise is to write them in hexadecimal, base sixteen, where the digits run from 0 to 9 and then A to F. Because sixteen is 2⁴, one hex digit is exactly four binary digits, and so a byte can conveniently be written as exactly two hex digits.

(A running theme across all of this is that many of the choices are arbitrary; in different times or places, other choices may have been made. Most likely, other choices were made, and they’re still in use somewhere. Virtually the only reliable constant is that any computer you will ever encounter will have bytes made out of eight bits. But even that wasn’t always the case.)

The Unix program xxd will print out bytes in a somewhat readable way. Here’s its output for a short chunk of English text.

100000000: 5468 6520 7175 6963 6b20 6272 6f77 6e20  The quick brown
200000010: 666f 7820 6a75 6d70 7320 6f76 6572 2074  fox jumps over t
300000020: 6865 206c 617a 7920 646f 6727 7320 6261  he lazy dog's ba
400000030: 636b 2e0a                                ck..

Each line shows sixteen bytes. The left column shows the position (or “offset”) in the data, in hex. (It starts at zero, because programmers like to start counting at zero; it makes various things easier.) The middle column shows the bytes themselves, written as two hex digits each, with just enough space that you can tell where the boundaries between bytes are. The right column shows the bytes interpreted as ASCII text, with any non-characters replaced with a ..

(ASCII is a character encoding, a way to represent text as bytes — which are only numbers — by listing a set of characters in some order and then assigning numbers to them. Text crops up in a lot of formats, and this makes it easy to spot at a glance. Alas, ASCII is only one of many schemes, and it only really works for English text, but it’s the most common character encoding by far and has some overlap with the runners-up as well.)

Since everything is made out of bytes, there are an awful lot of schemes for how to express various kinds of information as bytes. As a result, a byte is meaningless on its own; it only has meaning when something else interprets it. It might be a plain number ranging from 0 to 255; it might be a plain number ranging from −128 to 127; it might be part of a bigger number that spans multiple bytes; it might be several small numbers crammed into one byte; it might be part of a color value; it might be a letter.

A meaningful arrangement for a whole sequence of bytes is loosely referred to as a format. If it’s intended for an entire file, it’s a file format. A file containing only bytes that are intended as text is called a plain text file (or format); this is in contrast to a binary file, which is basically anything else.

Some file formats are very common and well-understood, like PNG or MP3. Some are very common but were invented behind closed doors, like Photoshop’s PSD, so they’ve had to be reverse engineered for other software to be able to read and write them. And a great many file formats are obscure and ad hoc, invented only for use by one piece of software. Programmers invent file formats all the time.

Reverse engineering a format is largely a matter of identifying common patterns and finding data that’s expected to be present somewhere. Of course, in cases like Photoshop’s PSD, the most productive approach is to make small changes to a file in Photoshop and then see what changed in the resulting PSD. That’s not always an option — say, if you’re working with a game for a handheld that won’t let you easily run modified games.

Okay, hopefully that’s enough of that and you can pick up the rest along the way!

Diamond and Pearl

Before Diamond and Pearl, all of veekun’s data was just copied from other sources. Like, when I was in high school, I would spend lunch in the computer lab meticulously copy/pasting the Gold and Silver Pokédex text from another website into mine. Hey, I started the thing when I was 12.

But then… something happened. I can’t remember what it was, which makes this a much less compelling story. I assume veekun got popular enough that a couple other Pokénerds found out about it and started hanging around. Then when Diamond and Pearl came out, they started digging into the games, and I thought that was super interesting, so I did it too.

This is what led veekun into being much more about ripped data, though its track record has been… bumpy.

The Nintendo DS header and filesystem

Everything in a computer is, on some level, a sequence of bytes. Game consoles and handhelds, being computers, also deal in bytes. A game cartridge is just a custom disk, and a ROM is a file containing all the bytes on that disk. (It’s a specific case of a disk image, like an ISO is for CDs and DVDs. You can take a disk image of a hard drive or a floppy disk or anything else, too; they’re all just bytes.)

But what are those bytes? That’s the fundamental and pervasive question. In the case of a Nintendo DS cartridge, the first thing I learned was that they’re arranged in a filesystem. Most disks have a filesystem — it’s like a table of contents for the disk, explaining how the one single block of bytes is divided into named files.

That is fantastically useful, and I didn’t even have to figure out how it works, because other people already had. Let’s have a look at it, because seeing binary formats is the best way to get an idea of how they might be designed. Here’s the beginning of the English version of Pokémon Diamond.

 100000000: 504f 4b45 4d4f 4e20 4400 0000 4144 4145  POKEMON D...ADAE
 200000010: 3031 0000 0900 0000 0000 0000 0000 0500  01..............
 300000020: 0040 0000 0008 0002 0000 0002 2477 1000  .@..........$w..
 400000030: 00d0 3000 0000 3802 0000 3802 1c93 0200  ..0...8...8.....
 500000040: 0064 3300 7f15 0000 007a 3300 200b 0000  .d3......z3. ...
 600000050: 00b8 1000 e00a 0000 0000 0000 0000 0000  ................
 700000060: 5766 4100 f808 1808 0086 3300 3159 7e0d  WfA.......3.1Y~.
 800000070: 740a 0002 5801 3802 0000 0000 0000 0000  t...X.8.........
 900000080: c05e a503 0040 0000 684b 0000 0000 0000  .^...@..hK......
1000000090: 0000 0000 0000 0000 0000 0000 0000 0000  ................
11000000a0: 0000 0000 0000 0000 0000 0000 0000 0000  ................
12000000b0: 0000 0000 0000 0000 0000 0000 0000 0000  ................
13000000c0: 24ff ae51 699a a221 3d84 820a 84e4 09ad  $..Qi..!=.......
14000000d0: 1124 8b98 c081 7f21 a352 be19 9309 ce20  .$.....!.R..... 
15000000e0: 1046 4a4a f827 31ec 58c7 e833 82e3 cebf  .FJJ.'1.X..3....
16000000f0: 85f4 df94 ce4b 09c1 9456 8ac0 1372 a7fc  .....K...V...r..

How do we make sense of this? Let us consult the little tool I started writing for this, porigon-z. It’s abandoned and unfinished and not terribly well-written; I would just link to the documentation I consulted when writing this, but it’s conspicuously 404ing now, so this’ll have to do. I described the format using an old version of the Construct binary format parsing library, and it looks like this:

 1nds_image_struct = Struct('nds_image',
 2    String('title', 12),
 3    String('id', 4),
 4    ULInt16('publisher_code'),
 5    ULInt8('unit_code'),
 6    ULInt8('device_code'),
 7    ULInt8('card_size'),
 8    String('card_info', 10),
 9    ULInt8('flags'),
10    ...

A String is text of a fixed length, either truncated or padded with NULs (character zero) to fit. The clumsy ULInt16 means an Unsigned, Little-endian, 16-bit (two byte) integer.

(What does little-endian mean? I’m glad you asked! When a number spans multiple bytes, there’s a choice to be made: what order do those bytes go in? The way we write numbers is big-endian, where the biggest part appears first; but most computers are little-endian, putting the smallest part first. That means a number like 0x1234 is actually stored in two bytes as 34 12.)

Alas, this is a terrible example, since most of this is goofy internal stuff we don’t actually care about. The interesting bit is the “file table”. A little ways down my description of the format is this block of ULInt32s, which start at position 0x40 in the file.

1file_table_offset   00 64 33 00 = 0x00336400
2file_table_length   7f 15 00 00 = 0x0000157f (5503)
3fat_offset          00 7a 33 00 = 0x00337a00
4fat_length          20 0b 00 00 = 0x00000b20 (2848)

Excellent. Now we know that if we start at 0x00336400 and read 5503 bytes, we’ll have the entire filename table.

 1003363f0: ffff ffff ffff ffff ffff ffff ffff ffff  ................
 200336400: 2802 0000 5700 4500 cd02 0000 5700 00f0  (...W.E.....W...
 300336410: f502 0000 5700 01f0 fd02 0000 5700 02f0  ....W.......W...
 400336420: 0b03 0000 5800 01f0 3203 0000 5a00 01f0  ....X...2...Z...
 500336430: 3e03 0000 5a00 05f0 7b03 0000 5d00 00f0  >...Z...{...]...
 600336440: cf03 0000 6300 00f0 f403 0000 6300 08f0  ....c.......c...
 700336450: 0b04 0000 6500 08f0 5804 0000 6a00 08f0  ....e...X...j...
 8...
 900336610: 0f15 0000 5d01 41f0 4315 0000 6101 41f0  ....].A.C...a.A.
1000336620: 6a15 0000 6301 41f0 8b61 7070 6c69 6361  j...c.A..applica
1100336630: 7469 6f6e 01f0 8361 7263 07f0 8662 6174  tion...arc...bat
1200336640: 746c 6508 f087 636f 6e74 6573 740d f084  tle...contest...
1300336650: 6461 7461 10f0 8464 656d 6f13 f083 6477  data...demo...dw
1400336660: 631d f089 6669 656c 6464 6174 611e f087  c...fielddata...
1500336670: 6772 6170 6869 632c f088 6974 656d 746f  graphic,..itemto
16...

I included one previous line for context; starting right after a whole bunch of ffs or 00s is a pretty good sign, since those are likely to be junk used to fill space. So we’re probably in the right place, or at least a right place. Also we’re definitely in the right place since I already know porigon-z works, but, you know.

The beginning part of this is a bunch of numbers that start out relatively low and gradually get bigger. That’s a pretty good indication of an offset table — a list of “where this thing starts” and “how long it is”, just like the offset/length pairs that pointed us here in the first place. The only difference here is that we have a whole bunch of them. And porigon-z confirms that this is a list of:

1    ULInt32('offset'),
2    ULInt16('top_file_id'),
3    ULInt16('parent_directory_id'),

My code does a bit more than this, but I don’t want this post to be about the intricacies of an old version of Construct. The short version is that each entry is eight bytes long and corresponds to a directory; this list actually describes the directory tree. Decoding the first few produces:

1offset 00000228, top file id 0057, parent id 0045
2offset 000002cd, top file id 0057, parent id f000
3offset 000002f5, top file id 0057, parent id f001
4offset 000002fd, top file id 0057, parent id f002
5...

Again, we encounter some mild weirdness. The parent ids seem to count upwards, except for the first one, and where did that f come from? It turns out that for the first record only — which is the root directory and therefore has no parent — the parent id is actually the total number of records to read. So there are 0x0045 or 69 records here. As for the f, well, I have no idea! I just discard it entirely when linking directories together.

So let’s fully decode entry 3 (the fourth one, since we started at zero). It has offset 0x000002fd, which is relative to where the table starts, so we need to add that to 0x00336400 to get 0x003366fd. We don’t have a length, but starting from there we see:

1003366f0:                                 0c 6362               .cb
200336700: 5f64 6174 612e 6e61 7263 000f 7769 6669  _data.narc..wifi
300336710: 5f65 6172 7468 2e6e 6172 6315 7769 6669  _earth.narc.wifi
400336720: 5f65 6172 7468 5f70 6c61 6365 2e6e 6172  _earth_place.nar
5...

I called the structure here a filename_list_struct. Also, as I read this code, I really wish I’d made it more sensible; sorry, I guess I’ll clean it up when I get around to re-ripping gen 4. The Construct code is a bit goofy, but the idea is:

• Read a byte. If it’s zero, stop here. Otherwise, the top bit is a flag indicating whether this entry is a directory; the rest is a length.
• The next length bytes are the filename.
• Iff this is a directory, the next two bytes are the directory id.
• Repeat.

(Ah yes, bits and flags. A flag is something that can only be true or false, so it really only needs one bit to store. So programmers like to cram flags into the same byte as other stuff to save space. Computers can’t examine individual bits directly, but it’s easy to manipulate them from code with a little math. Of course, using 1 bit for a flag means only 7 are left for the length, so it’s limited to 127 instead of 255.)

Let’s try this. The first byte is 0c. I can tell you right away that the top bit is zero; if the top bit is one, then the first hex digit will be 8 or greater. So this is just a file, and it’s 0c or 12 bytes long. The next twelve bytes are cb_data.narc, so that’s the filename. Repeat from the beginning: the next byte is 00, which is zero, so we’re done. This directory only contains a single file, cb_data.narc.

But wait, what is this directory? We know its id is 3; its name would appear somewhere in the filename list for its parent directory, 2, along with an extra two bytes indicating it matches to directory 3. To get the name for directory 2, we’d consult directory 1; and directory 1’s parent is directory 0. Directory 0 is the root, which is just / and has no name, so at that point we’re done. Of course, if we read all these filename lists in order rather than skipping straight to the third one, then we’d have already seen all these names and wouldn’t have to look them up.

One final question: where’s the data? All we have are filenames. It turns out the data is in a totally separate table at fat_offset — “FAT” is short for “file allocation table”. That’s a vastly simpler list of pairs of start offset and end offset, giving the positions of the individual files, and nothing else.

All we have to do is match up the filenames to those offset pairs. This is where the “top file id” comes in: it’s the id of the first file in the directory, and the others count up from there. This directory’s top file id is 0x57, so cb_data.narc has file id 0x57. (If there were a next file, it would have id 0x58, and so on.) Its data is given by the 0x57th (87th) pair of offsets.

Phew! We haven’t even gotten anywhere yet. But this is important for figuring out where anything even is. And you don’t have to do it by hand, since I wrote a program to do it. Run:

1python2 -m porigonz pokemon-diamond.nds list

To get output like this:

1/application/custom_ball/data
2   87 0x03810200 0x0381ef8c     60812 [  295] /application/custom_ball/data/cb_data.narc
3/application/wifi_earth
4   88 0x037b2400 0x037d7674    152180 [    8] /application/wifi_earth/wifi_earth.narc
5   89 0x037d7800 0x037d84c8      3272 [   19] /application/wifi_earth/wifi_earth_place.narc
6...

Hey, it’s our friend cb_data.narc, with its full path! On the left is its file id, 87. Next are its start and end offsets, followed by its filesize.

You may notice that before the filenames start, you’ll get a list of unnamed files. These are entries in the FAT that have no corresponding filename. I learned only recently that they’re code — overlays, in fact, though I don’t know what that means yet.

Now we can start looking at data and figuring it out. Finally.

NARCs and basic Pokémon data

This was fantastic. All the game data, nearly arranged into files, and even named sensibly for us. A goldmine. It didn’t used to be so easy, as we will see later.

Other people had already noticed the file /poketool/personal/personal.narc contains much of the base data about Pokémon. You’ll notice it has a “501” in brackets next to it, indicating that it’s actually a NARC file — a “Nitro archive”, Nitro being the original codename for the DS. This is a generic uncompressed container that just holds some number of sub-files — in this case, 501. The subfiles can have names, but the ones in this game generally don’t, so the only way to refer to them is by number.

You may also notice that evo.narc and wotbl.narc, in the same directory, are also NARCs with 501 records. It’s a pretty safe bet that they all have one record per Pokémon. That’s a little odd, since Pokémon Diamond only has 493 Pokémon, but we’ll figure that out later.

NARC is, as far as I can tell, an invention of Nintendo. I think it’s in other DS games, though I haven’t investigated any others very much, so I can’t say how common it is. It’s a very simple format, and it uses basically the same structure as the entire DS filesystem: a list of start/end offsets and a list of filenames. It doesn’t have the same directory nesting, so it’s much simpler, and also the filenames are usually missing, so it’s simpler still. But you don’t have to care, because you can examine the contents of a file with:

1python2 -m porigonz pokemon-diamond.nds cat -f hex /poketool/personal/personal.narc

This will print every record as an unbroken string of hex, one record per line. (I admit this is not the smartest format; it’s hard to see where byte boundaries are. Again, hopefully I’ll fix this up a bit when I rerip gen 4.) Here are the first six Pokémon records.

10000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
22d31312d41410c032d400001000000001f144603010741000003000020073584081e10022024669202000000
33c3e3f3c50500c032d8d0005000000001f144603010741000003000020073584081e10022024669202000000
45052535064640c032dd00006000000001f144603010741000003000030473586081e1002282466920a000000
527342b413c320a0a2d414000000000001f144603010e420000000000230651cce41e821201a4469202000000
63a403a5050410a0a2d8e4001000000001f144603010e420000000000230651cce41e821201a4469202000000

That first one is pretty conspicuous, what with its being all zeroes. It’s probably some a dummy entry, for whatever reason. That does make things a little simpler, though! Numbering from zero has caused some confusion in the past: Bulbasaur (National Dex number 1) would be record 0, and I’ve had all kinds of goofy bugs from forgetting to subtract or add 1 all over the place. With a dummy record at 0, that means Bulbasaur is 1, and everything is numbered as expected.

So, what is any of this? The heart of figuring out data formats is looking for stuff you know. That might mean looking for data you know should be there, or it might mean identifying common schemes for storing data.

A good start, then, would be to look at what I already know about Bulbasaur. Base stats are a pretty fundamental property, and Bulbasaur’s are 45, 49, 49, 65, 65, and 45. In hex, that’s 2d 31 31 41 41 2d. Hey, that’s the beginning of the first line! It’s just slightly out of order; Speed comes before the special stats.

You can also pick out some differences by comparing rows. About 60% of the way along the line, I see 03 for Bulbasaur, Ivysaur, and Venusaur, but then 00 for Charmander and Charmeleon. That’s different between families, which seems like a huge hint; does that continue to hold true? (As it turns out, no! It fails for Butterfree — because it indicates the Pokémon’s color, used in the Pokédex search. Most families are similar colors.)

Sometimes a byte will seem to only take one of a few small values, which usually means it’s an enum (one of a list of numbered options), like the colors are. A byte that only ranges from 1 to 17 (or perhaps 0 to 16) is almost certainly type, for example, since there are 17 types.

Noticing common patterns — very tiny formats, I suppose — is also very helpful (and saves you from wild goose chases). For example, Pokémon can appear in the wild holding held items, and there are more than 256 items, so referring to an item requires two bytes. But there are only slightly more than 256 items in this game, so the second byte is always 00 or 01. If you remember that some fields must span multiple bytes, that’s an incredible hint that you’re looking at small 16-bit numbers; if you forget, you might think the 01 is a separate field that only stores a single flag… and drive yourself mad trying to find a pattern to it.

The games have a number of TMs which can teach particular moves, and each Pokémon can learn a unique set of TMs. These are stored as a longer block of bytes, where each individual bit is either 1 or 0 to indicate compatibility. Those are a bit harder to identify with certainty, since (a) the set of TMs changes in every game so you can’t just check what the expected value is, and (b) bitflags can produce virtually any number with no discernible pattern.

Thankfully, there’s a pretty big giveaway for TMs in particular. Here are Caterpie, Metapod, and Butterfree:

12d1e232d14140606ff350100000000007f0f4600030313000003000000000000000000000000000000000000
23214371e1919060678482000000000007f0f460003033d000003000000000000000000000000000000000000
33c2d3246505006022da000060000de007f0f460003030e000008000020463fb480be14222830560301000000

Butterfree can learn TMs. Caterpie and Metapod are almost unique in that they can’t learn any. Guess where the TMs are! Even better, Caterpie is only #9, so this shows up very early on.

And, well, that’s the basic process. It’s mostly about cheating, about leveraging every possible trick you can come up with to find patterns and landmarks. I even wrote a script for this (and several other files) that dumped out a huge HTML table with the names of the (known) Pokémon on the left and byte positions as columns. When I figured something out, or at least had a suspicion, I labelled the column and changed that byte to print as something more readable (e.g., printing the names of types instead of just their numbers).

Of course, if you have a flash cartridge or emulator (both of which were hard to come by at the time), you can always invoke the nuclear option: change the data and see what changes in the game.

Still, easy, right? How hard could this be.

Sprites: In which it gets hard

What we really really wanted were the sprites. This was a new generation with new Pokémon, after all, and sprites were the primary way we got to see them. Unlike nearly everything else, this hadn’t already been figured out by other people by the time I showed up.

Finding them was easy enough — there’s a file named /poketool/pokegra/pokegra.narc, which is conspicuously large. It’s a NARC containing 2964 records. A little factoring reveals that 2964 is 494 × 6 — aha! There are 493 Pokémon, plus one dummy.

1python2 -m porigonz pokemon-diamond.nds extract /poketool/pokegra/pokegra.narc

This will extract the contents of pokegra.narc to a directory called pokemon-diamond.nds:data, which I guess might be invalid on Windows or something, so use -d to give another directory name if you need to. Anyway, in there you’ll find a directory called pokegra.narc, inside of which are 2964 numbered binary files.

Some brief inspection reveals that they definitely come in groups of six: the filesizes consistently repeat 6.5K, 6.5K, 6.5K, 6.5K, 72, 72. Sometimes a couple of the files are empty, but the pattern is otherwise very distinct. Four sprites per Pokémon, then?

Let’s have a look at the first file! Since it’s a dummy sprite, it should be blank or perhaps a question mark, right? Oh boy I’m so excited.

100000000: 5247 434e fffe 0001 3019 0000 1000 0100  RGCN....0.......
200000010: 5241 4843 2019 0000 0a00 1400 0300 0000  RAHC ...........
300000020: 0000 0000 0100 0000 0019 0000 1800 0000  ................
400000030: de54 59cf e00a 2374 927c 5db5 7476 87c1  .TY...#t.|].tv..
500000040: 06d1 2183 c890 ab40 3a06 a53c dced 8f55  ..!....@:..<...U
600000050: 2e90 e9a5 b0e1 3324 e2a2 ed42 4480 9790  ......3$...BD...
700000060: 5632 b157 989d bb3e 8af2 35e8 accd 9f92  V2.W...>..5.....
800000070: 7e57 79b8 8064 43b0 3295 7d4c 1476 a77b  ~Wy..dC.2.}L.v.{
9...

Hm. Okay, so, this is a problem. No matter what the actual contents are, this is a sprite, and virtually all Pokémon sprites have a big ol’ blob of completely empty space in the upper-left corner. Every corner, in fact. Except for a handful of truly massive species, the corners should be empty. So no matter what scheme this is using or what order the pixels are in, I should be seeing a whole lot of zeroes somewhere. And I’m not.

Compression? Seems very unlikely, since every file is either 0, 72, or 6448 bytes, without exception.

Well, let’s see what we’ve got here. RGCN and RAHC are almost certainly magic numbers, so this is one file format nested inside another. (A lot of file formats start with a short fixed string identifying them, a so-called “magic number”. Every GIF starts with the text GIF89a, for example. A NARC file starts with CRAN — presumably it’s “backwards” because it’s being read as an actual little-endian number.) I assume the real data begins at 0x30.

Without that leading 0x30 (48) bytes, the file is 6400 bytes large, which is a mighty conspicuous square number! Pokémon sprites have always been square, so this could mean they’re 80×80, one byte per pixel. (Hm, but Pokémon sprites don’t need anywhere near 256 colors?)

I see a 30 in the first line, which is probably the address of the data. I also see a 10, which is probably the (16-bit?) length of that initial header, or the address of the second header. What about in the second header? Well, uh, hm. I see a lot of what seem to be small 16-bit or 32-bit numbers: 0x000a is 10, 0x0014 is 20, 0x0003 is 3; 0x0018 is 24. A quick check reveals that 0x1900 is 6400 (the size of the data), and so 0x1920 is the size of the data plus this second header.

This hasn’t really told me anything I don’t already know. It seems very conspicuous that there’s no 0x50, which is 80, my assumed size of the sprite.

Well, hm, let’s look at the second file. It’s in the block for the same “Pokémon”, so maybe it’ll provide some clues.

Ah. No. It starts out completely identical. In fact, md5sum reveals that all four of these first sprites are identical. Might make sense for a dummy Pokémon. Does that pattern hold for the next Pokémon, which I assume is Bulbasaur? Not quite! Files 6 and 7 are identical, and 8 and 9 are identical, but they’re distinct from each other.

What’s the point of them then? Further inspection reveals that most Pokémon have paired sprites like this, but Pikachu does not — suggesting (correctly) that the sprites are male versus female, so Pokémon that don’t have gender differences naturally have identical pairs of sprites.

Okay, then, let’s look at Pikachu’s first sprite, 150. The key is often in the differences, remember. If the dummy sprite is either blank or a question mark, then it should still have a lot of corner pixels in common with the relatively small Pikachu.

100000030: b6bd 6f4c 6c6e 3d16 b226 db0b 0818 c934  ..oLln=..&.....4
200000040: eeb7 876c e41f 9542 6a6d 73da 0022 a1cb  ...l...Bjms.."..
300000050: 2683 9f01 5cfa ed9b 2275 0bce f8c4 79bf  &...\..."u....y.
400000060: 5eff b76b d4dd 4582 da1d a346 f0e0 5170  ^..k..E....F..Qp
500000070: 960c cf0a 4caa 9d55 9247 3ba4 e855 293e  ....L..U.G;..U)>
600000080: ce8a e73e c43f f575 4ad2 d346 e003 0189  ...>.?.uJ..F....
700000090: 065a ff67 3c7e 4d43 029e 6b8e d8ca d9b0  .Z.g<~MC..k.....
8000000a0: 3e5a 17e6 b445 a51d ba8a 03db d08a b115  >Z...E..........

Well. Nope. How does that compare to Pikachu’s second sprite, 151 — which ought to be extremely similar, seeing as the only gender difference is a notch in the tail?

100000030: 2957 ce67 e76f c494 f5fe 4adf d367 e008  )W.g.o....J..g..
200000040: 0182 0697 ff78 3c33 4dac 020b 6b8f d82f  .....x<3M...k../
300000050: d989 3ef7 17d7 b45a a566 ba57 03bc d04f  ..>....Z.f.W...O
400000060: b1ce 7668 2fea 2ceb fd8d 72a5 9b4d c848  ..vh/.,...r..M.H
500000070: 89b0 aeca 4712 a4c4 5582 2ad4 33a4 c0fa  ....G...U.*.3...
600000080: 618f e6fd 5faf 1cc7 ada3 e2c3 cb1f b845  a..._..........E
700000090: 39cb 1ee2 7721 94d2 0552 9a54 6320 b009  9...w!...R.Tc ..
8000000a0: 11c4 5657 8fc8 0cc7 5ded 5266 fb05 a826  ..VW....].Rf...&

Oh, my god. Nothing is similar at all.

Make a histogram? Every possible value appears with roughly the same frequency. Now that is interesting, and suggests some form of encryption — most likely one big “mask” xor’d with the whole sprite. But how to find the mask?

(It doesn’t matter exactly what xor is, here. It only has two relevant properties. One is that it’s self-reversing, making it handy for encryption like this — (data xor mask) xor mask produces the original data. The other is that anything xor’d with zero is left unchanged, so if I think the original data was zero — as it ought to be for the blank pixels in the corners of a sprite — then the encrypted data is just the mask! So I know at least the beginning parts of the mask for most sprites; I just have to figure out how to use a little bit of that to reconstitute the whole thing.)

I stared at this for days. I printed out copies of sprite hex and stared at them more on breaks at work. I threw everything I knew, which admittedly wasn’t a lot, at this ridiculous problem.

And slowly, some patterns started to emerge. Consider the first digit of the last column in the above hex dump: it goes e, d, d, c, c, b, b, a. In fact, if you look at the entire byte, they go e0, d8, d0, c8, etc. That’s just subtracting 08 on each row.

Are there other cases like this? Kinda! In the third column, the second digit alternates between 7 and f; closer inspection reveals that byte’s increasing by 18 every row. Oh, the sixth column too. Hang on — in every column, the second digit alternates between two values. That seems true for every other file we’ve seen so far, too.

This is extremely promising! Let’s try this. Take the first two rows, which are bytes 0–15 and bytes 16–31. Subtract the second row from the first row bytewise, making a sort of “delta row”. For the second Pikachu, that produces:

1d82b 3830 1809 789f 58ae b82c 9828 f827

As expected, the second digit in each column is an 8. Now just start with the first row and keep adding the delta to it to produce enough rows to cover the whole file, and xor that with the file itself. Results:

100000000: 0000 0000 0000 0000 0000 0000 0000 0000  ................
200000010: 0000 0000 0000 0000 0000 0000 0000 0000  ................
300000020: 0024 0030 0056 0088 003c 0060 000b 0019  .$.0.V...<.`....
400000030: 0016 009f 0060 009a 0085 00c6 0092 0035  .....`.........5
500000040: 00b3 00ed 0081 00d4 0034 005b 00a3 005e  .........4.[...^
600000050: 00a1 00aa 0033 0068 00c7 0078 0030 008e  .....3.h...x.0..
700000060: 0092 0065 0084 009c 0040 00b3 0077 00fb  ...e.....@...w..
800000070: 0040 00e0 0066 002a 002d 0075 007a 003f  .@...f.*.-.u.z.?
900000080: 0076 00da 00b3 0008 00bb 00e6 0097 003c  .v.............<

Promising! We got a bunch of zeroes, as expected, though everything else is still fairly garbled. It might help if we, say, printed this out to a file.

By now it had become clear that the small files were palettes of sixteen colors stored as RGB555 — that is, each color is packed into two bytes, with five bits each for the red, green, and blue channels. Sixteen colors means two pixels can be crammed into a single byte, so the sprites are actually 160×80, not 80×80. Combining this knowledge with the above partially-decrypted output, we get:

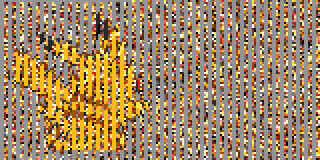
Success!

Kinda!

Meanwhile another fansite found our code and put up a full set of these ugly-ass corrupt sprites, so that was nice.

It took me a while to notice another pattern, which emerges if you break the sprite into blocks that are 512 bytes wide (rather than only 16). You get this:

12957 ce67 e76f c494 f5fe 4adf d367 e008 ...
229e2 ce3e e742 c4d3 f5d9 4a46 d30a e057 ...
3296d ce15 e715 c412 f5b4 4aad d3ad e0a6 ...
429f8 ceec e7e8 c451 e561 a450 9763 e7f5 ...

This time, the byte in the first column is always identical all the way down. Well, kind of. This is encrypted data, remember, and I only know what the mask is because the beginning of the data is usually blank. The exceptions are when the mask is hitting actual colored pixels, at which point it becomes garbage.

But even better, look at the second byte in each column. Now they’re all separated by a constant, all the way down! That means I can repeat the same logic as before, except with two “rows” that are 512 bytes long, and as long as the first 1024 bytes of the original data are all zeroes, I’ll get a perfect sprite out!

And indeed, I did! Mostly. Legendary Pokémon and a handful of others tend to be quite large, so they didn’t start with as many zeroes as I needed for this scheme to work. But it mostly worked, and that was pretty goddamn cool.

magical, a long-time co-conspirator, managed to scrounge up my final “working” code from that era (which then helped me find my own local copy of all my D/P research stuff, which I oughta put up somewhere). It’s total nonsense, but it came pretty close to working.

…

Hm? What? You want to know the real answer? Yeah, I bet you do.

Okay, here you go. So the games have a random number generator, for… generating random numbers. This being fairly simple hardware with fairly simple (non-crypto) requirements, the random number generator is also fairly simple. It’s an LCG, a linear congruential generator, which is a really bizarre name for a very simple idea:

The generator is defined by the numbers a and b. (You have to pick them carefully, or you’ll get numbers that don’t look particularly random.) You pick a starting number (a seed) and call that x. When you want a random number, you compute ax + b. You then take a modulus, which really means “chop off the higher digits because you only have so much space to store the answer”. That’s your new x, which you’ll plug in to get the next random number, and so on.

In the case of the gen 4 Pokémon games, a = 0x4e6d and b = 0x6073.

What does any of this have to do with the encryption? Well! The entire sprite is interpreted as a bunch of 16-bit integers. The last one is used as the seed and plugged into the RNG, and then it keeps spitting out a sequence of numbers. Reverse them, since you’re starting at the end, and that’s the mask.

The seed technically overlaps with the last four pixels, but it happens to work since no Pokémon sprites touched the bottom-right corner in Diamond and Pearl. In Platinum a couple very large sprites broke that rule, so they ended up switching this around and starting from the beginning. Same idea, though.

Of course, porigon-z knows how to handle this… though it’s currently hardcoded to use the Platinum approach. Funny story: the algorithm was originally thought to go from the beginning, not the end, and it used an LCG with different constants. Turns out someone had just discovered the reverse of the Pokémon LCG, which would produce exactly the same sequence, backwards. Super cool.

I am a little curious: why were the sprites encrypted in the first place? What possible point is there? They must have known we cracked the encryption, but then they used it again for Platinum, and again Heart Gold and Soul Silver. Maybe it was only intended to be enough to delay us, during the gap between the Japanese and worldwide releases…? Hm.

Incidentially, the entire game text is also encrypted in much the same way. Without the encryption, it’s just UTF-16 — a common character encoding that uses two bytes for every character. I have no idea what the encryption is for, or why it’s still used in Sun and Moon.

Oh hey, so. Why did that thing with subtracting the two rows kinda-sorta work? Well! That’s a very good question that I only just recently bothered looking into.

SOME MATH

I think it’s because of one of the rules for choosing good factors for an LCG — in particular, a - 1 should be divisible by 4, or the LCG won’t run through all possible values. That means a can be written as 4m + 1, for some integer m. I’ll come back to this in a moment.

First, consider what happens when you start with a value x and run it through the LCG a few times. At this point I apologize for not having MathJax or something on this blog, but oh well.

1step 0: x
2step 1: ax + b
3step 2: a(ax + b) + b = a²x + ab + b
4step 3: a(a²x + ab + b) + b = a³x + a²b + ab + b
5...
6step n: aⁿ x + (aⁿ⁻¹ + aⁿ⁻² + ... + a² + a + 1) b
7      = aⁿ x + (aⁿ - 1) / (a - 1) b

(That last step is a pretty common trick; you can do the multiplication yourself if you don’t believe me.)

I’m going to restrict the cases we care about to when n is a power of two, because powers of two are interesting. Let’s say it’s, I dunno, 8. So we have some a⁸ terms in there. That’s equivalent to squaring a three times. We know a is 4m + 1, so let’s try squaring that repeatedly.

1a² = (4m + 1)² = 16m² + 8m + 1
2a⁴ = (16m² + 8m + 1)² = 256m⁴ + 256m³ + 96m² + 16m + 1
3a⁸ = ?!

An interesting pattern emerges! a² - 1 is divisible by 8, and a⁴ - 1 is divisible by 16. It wouldn’t be outrageous to assume that a⁸ - 1 is divisible by 32.

But we can do one better: a² - 1 is actually divisible by 8m, and a⁴ - 1 is divisible by 16m, and of course a⁸ - 1 is divisible by 32m. In other words, we can write a⁸ as 32mj + 1, where j is a bunch of junk we don’t care about.

Now let’s look at the formula for step 8 and replace some of those as.

1a⁸ x + (a⁸ - 1) / (a - 1) b
2= (32mj + 1) x + (32mj) / (4m) b
3= 32mjx + x + 8jb
4= 8(4mjx + jb) + x

Aha! All of these variables are integers, so this is 8, times a bunch of garbage, plus the original number x. Or in other words, by feeding x through the LCG eight times, we know it increases by a multiple of eight.

And that explains almost everything. This particular LCG operates two bytes at a time, so when you look down columns in xxd‘s sixteen byte wide output, you’re seeing values that are eight steps apart. Repeatedly adding eight (or an odd multiple of eight) to a number in hex will cause the last digit to alternate between two values, just like repeatedly adding five to a number in decimal. (But why did the digits alternate down the second column? Because these are little-endian two-byte numbers, so the “last” or smallest digit appears at the end of the first byte.)

Similarly, comparing bytes that are 512 apart is the same as comparing two-byte numbers that are 256 steps apart. You can repeat the same logic to find that after 256 steps, you get 256 times a bunch of garbage, plus x. So the last byte will always be unchanged. 256 is 0x100 in hex, so in hex it has the same “shifting to the left” powers as 100 has in decimal.

I did gloss over two minor things. One, why does the value specifically increase by an odd multiple of eight every eight steps? That’s because 4mjx + jb happens to be odd: 4mjx is obviously even, j is always odd (if you look at what it must be for a² and a⁴, you’ll see it’s a lot of even terms plus one at the end), and for this particular LCG, b is also odd. If b were even, you’d have sixteen times some garbage plus x, and so the smallest hex digit would remain the same after eight steps.

And two, why can I take the same garbage and keep adding it repeatedly to skip ahead 256 steps at a time, when the garbage depends on the previous value x? Well, let’s see what happens when you take step 256 and plug it back into itself:

1step 0: x
2step 256: 256(4mjx + jb) + x
3step 512: 256(4mj(256(4mjx + jb) + x) + jb) + (256(4mjx + jb) + x)
4        = 256(256(4mj)(4mjx + jb) + 4mjx + jb) + 256(4mjx + jb) + x
5    = 65536(4mj)(4mjx + jb) + 256(4mjx + jb) + 256(4mjx + jb) + x
6    = 65536(4mj)(4mjx + jb) + 512(4mjx + jb) + x

That huge term on the left is divisible by 65536, which is 0x10000 in hex — in other words, no matter what it is, adding it on can’t change the last four hex digits. The LCG only spits out four hex digits, so no matter what all of that stuff is, it won’t make any difference. And once you throw that away, what’s left is… the same expression for step 256, except that the garbage term has been doubled! We can find the garbage term by subtracting step 0 from step 256 to cancel out the lone x, and then we can add it to step 256 to get step 512. By the same reasoning, we can add it again to get step 768, then step 1024, and so on.

I hope that clears that up.

The dark days

So Nintendo DS cartridge have a little filesystem on them, making them act kinda like any other disk. Nice.

Game Boy cartridges… don’t. A Game Boy cartridge is essentially just a single file, a program. You pop the cartridge in, and the Game Boy runs that program.

Where is the data, then? Baked into the program — referred to as hard-coded. Just, somewhere, mixed in alongside all the program code. There’s no nice index of where it is; rather, somewhere there’s some code that happens to say “look at the byte at 0x006f9d10 in this program and treat it as data”.

I wasn’t involved in data dumping in these days; I was copying stuff straight out of the wildly inaccurate Prima strategy guide. (Again, you know, I was 12.) It’s hard to say exactly how people fished out the data, though I can take a few guesses.

A few guesses

To our advantage is the fact that Game Boy cartridges are much smaller than DS cartridges, so there’s much less to sift through. Pokémon Red and Blue are on 1 MB cartridges, and even those are half empty (unused NULs); the original Japanese Red and Green barely fit into 512 KB, and Red and Blue ended up just slightly bigger.

To our disadvantage is that these are the very first games, so we don’t have any pre-existing knowledge to look for. We don’t know any Pokémon’s base stats; we may not even know that “base stats” are a thing yet. Also, it’s not immediately obvious, but the Pokémon aren’t even stored in order. Oh, and Mew is completely separate; it really was a last-minute addition.

What do we know? Well, by playing the game, we can see what moves a Pokémon learns and when. There don’t seem to be all that many moves, so it’s reasonable to assume that a move would be represented with a single byte. Levels are capped at 100, so that’s probably also a single byte. Most likely, the level-up moves are stored as either level move level move... or move level move level....

Great! All we need to do is put together a string of known moves both ways and find them.

Except, ah, hm. We don’t actually know how the moves are numbered. But we still know the levels, so maybe we can get somewhere. Let’s take Bulbasaur, which we know learns Leech Seed at level 7, Vine Whip at level 13, and Poison Powder at level 20. (Or, I guess, that should be LEECH SEED, VINE WHIP, and POISONPOWDER.) No matter whether the levels or moves come first, this will result in a string like:

107 ?? 0D ?? 14

So we can do my favorite thing and slap together a regex for that. (A regex is a very compact way to search text — or bytes — for a particular pattern. A lone . means any single character, so the regex below is a straightforward translation of the pattern above.)

1>>> for match in re.finditer(rb'\x07.\x0d.\x14', rom):
2...     print(f"{match.start():08x} {match.group().hex()}")
3... 
40003b848 07490d1614

Exactly one match! Let’s have a look at that position in the file.

10003b840: 7700 0000 0110 0900 0749 0d16 144d 1b4b  w........I...M.K
20003b850: 224a 294f 304c 0000 0749 0d16 164d 1e4b  "J)O0L...I...M.K
30003b860: 2b4a 374f 414c 0000 0730 0d23 1228 1637  +J7OAL...0.#.(.7
40003b870: 1b84 2370 2b67 3238 0000 0001 219e 0013  ..#p+g28....!...

This seems pretty promising! It looks like the same set of moves is repeated 16 bytes later, but with different (slightly higher) levels after a certain point, which matches how evolved Pokémon behave. So this looks to be at least Bulbasaur and Ivysaur, though I’m not quite sure what happened to Venusaur.

By repeating this process with some other Pokémon, we can start to fill in a mapping of moves to their ids. Eventually we’ll realize that a Pokémon’s starting moves don’t seem to appear within this structure, and so we’ll go searching for those for a Pokémon that starts with moves we know the ids for. That will lead us to the basic Pokémon data along with base stats, because starting moves happen to be stored there in these early games.

The text isn’t encrypted, but also isn’t ASCII, but it’s possible to find it in much the same way by treating it as a cryptogram (or a substitution cipher). I assume that there’s some consistent scheme, such that the letter “A” is always represented with the same byte. So I pick some text that I know has a few repeated letters, like BULBASAUR, and I recognize that it could be substituted in some way to read as 123145426. I can turn that into a regex!

1>>> for match in re.finditer(rb'(.)(.)(.)\1(.)(.)\4\2(.)', rom, flags=re.DOTALL):
2...     print(f"{match.start():08x} {match.group().hex()}")

Unfortunately, this produces a zillion matches, most of them solid strings of NUL bytes. The problem is that nothing in the regex requires that the different groups are, well, different. You could write extra code to filter those cases out, or if you’re masochistic enough, you could express it directly within the regex using (?!...) negative lookahead assertions:

 1>>> for match in re.finditer(rb'(.)(?!\1)(.)(?!\1)(?!\2)(.)\1(?!\1)(?!\2)(?!\3)(.)(?!\1)(?!\2)(?!\3)(?!\4)(.)\4\2(?!\1)(?!\2)(?!\3)(?!\4)(?!\5)(.)', rom, flags=re.DOTALL):
 2...     print(f"{match.start():08x} {match.group().hex()}")
 3...
 40000820c 4305ff43441b440522
 50001c80e 81948b818092809491
 600054a94 0a4d350a556d554d43
 70007a55a 33466f33fff0ff4670
 80007c20c 4305e843440444050b
 90008e7b2 7fa8b37fa0a6a0a8ad
1000094e75 81948b818092809491
11000a0bcd a77fb3a7a4b1a47fb6

That’s much more reasonable. (The set of matches, I mean, not the regex.) It wouldn’t be hard to write a script with a bunch of known strings in it, generate appropriate regexes for each, eliminate inconsistent matches, and eventually generate a full alphabet. (Or you could assume that “B” immediately follows “A” and in general the letters are clustered together, which would lead you to correctly suspect that the strings at 0x0001c80e and 0x00094e75 are the ones you want.)

Even better, once you have an alphabet, you can use it to translate entire ROM — plenty of it will be garbage, but you’ll find quite a lot of blocks of human-readable text! And now you have all the names of everything and also the entire game script.

Modern day and a brief tour of gbz80 assembly

But like I said, I wasn’t involved in any of that. Until recently! I’ve been working on an experiment for veekun where I re-dump all the games to a new YAML-based format. Long story short: the current database is a pain to work with, and some old data has been lost entirely. Also, most of the data was extracted bits at a time with short hacky scripts that we then threw away, and I’d like to have more permanent code that can dump everything at once. It’ll be nice to have an audit trail, too — multiple times in the past, we’ve discovered that some old thing was dumped imperfectly or copied from an unreliable source.

So I started re-dumping Red and Blue, from scratch. I’ve made modest progress, though it’s taken a backseat to Sun and Moon lately.

It’s helped immensely that there’s an open source disassembly of Red and Blue floating around. What on earth is a disassembly? I’m so glad you asked!

Game Boy games were written in assembly code, which is just about as simple and painful as you can get. It’s human-readable, kinda, but it’s built from the basic set of instructions that a particular CPU family understands. It can’t directly express concepts like “if this, do that, otherwise do something else” or “repeat this code five times”. Instead, it’s a single long sequence of basic operations like “compare two numbers” and “jump ahead four instructions”. (Very few programmers work with assembly nowadays, but for various reasons, no other programming languages would work on the Game Boy at the time.)

To give you a more concrete idea of what this is like to work with: the Game Boy’s CPU doesn’t have an instruction for multiplying, so you have to do it yourself by adding repeatedly. I thought that would make a good example, but it turns out that Pokémon’s multiply code is sixty lines long. Division is even longer! Here’s something a bit simpler, which fills a span of memory:

 1FillMemory::
 2; Fill bc bytes at hl with a.
 3    push de
 4    ld d, a
 5.loop
 6    ld a, d
 7    ld [hli], a
 8    dec bc
 9    ld a, b
10    or c
11    jr nz, .loop
12    pop de
13    ret

CPUs tend to have a small number of registers, which can hold values while the CPU works on them — even as fast as RAM is, it’s considered much slower than registers. The downside is, well, you only have a few registers. The Game Boy CPU (a modified Z80) has eight registers that can each hold one byte: a through f, plus h and l.. They can be used together in pairs to store 16-bit values, giving the four combinations af, bc, de, and hl.

(If you need more than 16 bits, well, that’s your problem! 16 bits is the most the CPU understands; it can’t even access memory addresses beyond that range, so you’re limited to 64K. “But wait”, you ask, “how can a Game Boy cartridge be 512K or 1M?” Very painfully, that’s how.)

Now we can understand the comment in the above code. Starting at the memory address given by the 16-bit number in hl, it will copy the value in a into each byte, for a total of bc bytes. Translated into English, the above means something like this:

1. Save copies of d and e, so I can mess with them without losing any important data that was in them. (This code doesn’t use e, but there’s no push d instruction.)
2. Copy a, the fill value, into d.
3. Copy d, the fill value, into a.
4. Copy a, the fill value, into the memory at address hl. Then increase hl (the actual registers, not the memory) by 1.
5. Decrease bc, the number of bytes to fill, by 1.
6. Copy b, part of the number of bytes to fill, into a.
7. OR a with c, the other part of the number of bytes to fill, and leave the result in a. The result will be zero only if bc itself is zero, in which case the “zero” flag will be set.
8. If the zero flag is not set (i.e., if bc isn’t zero, meaning we’re not done yet), jump back to the instruction marked by .loop, which is step 3.
9. Restore d and e to their previous values.
10. Return to whatever code jumped here in the first place.

Even this relatively simple example has to resort to a weird trick — ORing b and c together — just to check if bc, a value the CPU understands, is zero or not.

CPUs don’t execute assembly code directly. It has to be assembled into machine code, which is (surprise!) a sequence of bytes corresponding to CPU instructions. When the above code is compiled, it produces these bytes, which you can verify for yourself appear in Pokémon Red and Blue in exactly one place:

1d5 57 7a 22 0b 78 b1 20 f9 d1 c9

I stress that this is way beyond anything virtually any programmer actually needs to know. Even the few programmers working with assembly, as far as I know, don’t usually care about the actual bytes that are spat out. I’ve actually had trouble tracking down lists of opcodes before — almost no one is trying to read machine code. We are out in the weeds a bit here.

To finally answer your hypothetical question: disassembly is the process of converting this machine code back into assembly. Most of it can be done automatically, but it takes extra human effort to make the result sensible. Let’s consult the Game Boy CPU’s (rather terse) opcode reference and see if we can make sense of this, pretending we don’t know what the original code was.

Find d5 in the table — it’s in row Dx, column x5. That’s push de. The first number in the box is 1, meaning the instruction is only one byte long, so the next instruction is the very next byte. That’s 57, which is ld d, a. Keep on going. Eventually we hit 20, which is jr nz, r8 and two bytes long — the notes at the bottom explain that r8 is 8-bit signed data. That means the next byte is part of this instruction; it’s f9, but it’s signed, so really that’s -7. We end up with:

 1push de
 2ld d, a
 3ld a, d
 4ld (hl+), a
 5dec bc
 6ld a, b
 7or c
 8jr nz, $-07
 9pop de
10ret

This looks an awful lot like what we started with, but there are a couple notable exceptions. First, the FillMemory:: line is completely missing. That’s just another kind of label, and the only way to know that the first line should be labelled at all is to find some other place in the code that tries to jump here. Given just these bytes, we can’t even tell if this is a complete snippet. Once we find that out, there’s still no way to recover the name FillMemory; even that is just a fan name and not the name from the original code. Someone came up with that name by reading this assembly code, understanding what it’s intended to do, and giving it a name.

Second, the .loop label is missing. The jr line forgot about the label and ended up with a number, which is how many bytes to jump backwards or forwards. (You can imagine how a label is much easier to work with than a number of bytes, especially when some instructions are one byte long and some are two!) An automated disassembler would be smart enough to notice this and would put a label in the right place. A really good disassembler might even recognize that this code is a simple loop that executes some number of times, and name that label .loop; otherwise, or for more complicated kinds of jumps, it would have a meaningless name that a human would have to improve.

And there’s a whole project where people have done the work of restoring names like this and splitting code up sensibly! The whole thing even assembles into a byte-for-byte identical copy of the original games. It’s really quite impressive, and it’s made tinkering with the original games vastly more accessible. You still have to write assembly, of course, but it’s better than editing machine code. Imagine trying to add a new instruction in the middle of the loop above; you’d screw up the jr‘s byte count, and every single later address in the ROM.

But more relevant to this post, a disassembly makes it easy to figure out where data is, since I don’t have to go hunting for it! When the code is assembled, it can generate a .sym file, which lists every single “global” label and the position it ended up in the final ROM. Many of those labels are for functions, like FillMemory is, but some of them are for blocks of data.

Snagging data

I set out to write some code to dump data from Game Boy games. Red/Green, Red/Blue, and Yellow were all fairly similar, so I wanted to use as much of the same code as possible for all of those games (and their various translations).

A very early pain point was, well, the existence of all those translations. Because there’s no filesystem, the only obvious way to locate data is to either search for it (which requires knowing it ahead of time, a catch-22 for a script that’s meant to extract it) or to bake in the addresses. The games contain quite a lot of data I want, and they exist in quite a few distinct versions, so that would make for a lot of addresses.

Also, with a disassembly readily available, it was now (relatively) easy for people to modify the games as they saw fit, in much the same way as it’s easy to modify most aspects of modern games by changing the data files. But if I simply had a list of addresses for each known release, then my code wouldn’t know what to do with modified games. It’s not a huge deal — obviously I don’t intend to put fan modifications into veekun — but it seemed silly to write all this extraction code and then only have it work on a small handful of specific files.

I decided to at least try to find data automatically. How can I do that, when the positions of the data only existed buried within machine code somewhere?

Obviously, I just need to find that machine code. See, that whole previous section was actually relevant!

I set out to do that. Remember the goofy regex from earlier, which searched for particular patterns of bytes? I did something like that, except with machine code. And by machine code, I mean assembly. And by assembly, I mean— okay just look at this.

1    ld a, [#wd11e]
2    dec a
3    ld hl, #TechnicalMachines
4    ld b, $0
5    ld c, a
6    add hl, bc
7    ld a, [hl]
8    ld [#wd11e], a
9    ret

I wrote my own little assembler that can convert Game Boy assembly into Game Boy machine code. The difference is that when it sees something like #foo, it assumes that’s a value I don’t know yet and sticks in a regex capturing group instead. It’s smart enough to know whether the value has to be one or two bytes, based on the instruction. It also knows that if the same placeholder appears twice, it must have the same value both times. I can also pass in a placeholder value, if I only know it at runtime.

I have half a dozen or so chunks like this. Every time I wanted to find something new, I went looking for code that referenced it and copied the smallest unique chunk I could (to reduce the risk that the code itself is different between games, or in a fan hack). I did run into a few goofy difficulties, such as code that changed completely in Yellow, but I ended up with something that seems to be pretty robust and knows as little as possible about the games.

I even auto-detect the language… by examining the name of the TOWN MAP, the first item that has a unique name in every official language.

This is probably ridiculous overkill, but it was a blast to get working. It also leaves the door open for some… shenanigans I’ve wanted to do for a while.

But enough about the Game Boy. Let’s get back to the future.

The 3DS, and what I'm doing now

Recent games have been slightly more complicated, though the complexity is largely in someone else’s court. The 3DS uses encryption — real, serious encryption, not baby stuff you can work around by comparing rows of bytes.

When X and Y came out, the encryption still hadn’t been broken, so all of veekun’s initial data was acquired by… making a Google Docs spreadsheet and asking for volunteers to fill it in. It wasn’t great, but it was better than nothing.

This was late 2013, and I suppose it’s around when veekun’s gentle decline into stagnation began. When X and Y were finally ripped, I was… what was I doing? I guess I was busy at work? For whatever reason, I had barely any involvement in it. Then Omega Ruby and Alpha Sapphire came out, and now everyone was busy, and it took forever just to get stuff like movesets dumped.

Now I’m working on Sun and Moon again. It’s not especially hard — much of the basic structure has been preserved since Diamond and Pearl, and a lot of the Omega Ruby and Alpha Sapphire code I wrote works exactly the same with Sun and Moon — but there are a lot of edge cases.

Some changes in X/Y and beyond

The most obvious wrinkle is that the filenames are gone. This has actually been the case since Heart Gold and Soul Silver — all the files now simply have names like /a/0/0/0 and count upwards from there. I don’t know the reason for the change, but I assume the original filenames weren’t intended to be left in the game in the first place. The files move around in every new pair of games, too, requiring bunches of people to go through the files by hand and note down what each of them appears to be.

Newer games use GARC instead of NARC. The G is apparently for Game Freak, so they must have decided Nintendo’s own format wasn’t good enough. It’s basically the same idea, except that now a single GARC archive has two levels of nesting — that is, a GARC contains some number of sub-archives, and each of those in turn contains some number of subfiles. Usually there’s only one subfile per subarchive, but I’ve seen zanier schemes once or twice.

Also, just in case that’s not enough levels of containers for you, there are also a number of other single-level containers embedded inside GARCs. They’re all very basic and nearly identical: just a list of start and end offsets.

Oh, and some of the data is compressed now. (Maybe that was the case before X/Y? I don’t remember.) Compression is fun. Any given data might be compressed with one of two flavors of LZSS, and it seems completely arbitrary what’s compressed and what’s not. There’s no indication of what’s compressed or what’s not, either; the only “header” that compressed data has is that the first byte is either 0x10 or 0x11, which isn’t particularly helpful since plenty of valid data also begins with one of those bytes.

But there was one much bigger practical problem with X and Y, one I’d been dreading for a while. X and Y, you see, use models — which means they don’t have any sprites for us to rip at all. And that kind of sucks.

The community’s solution has been for a few people (who have screen-capture hardware) to take screenshots and cut them out. It works, but it’s not great. The thing I’ve wanted for a very long time is rips of the actual models.

(Later games went back to including “sprites” that are just static screenshots of the models. Maybe out of kindness to us? Okay, yeah, doubtful. Oh, and those sprites are in the incredibly obtuse ETC1 format, which I had never heard of and needed help to identify, and which I will let you just read about yourself.)

Extracting models

The Pokémon models are an absolute massive chunk of the game data. All the data combined is 3GB; the Pokémon models are a hair under half of that, despite being compressed.

At least this makes them easy to find, since they’re all packed into a single GARC file.

That file contains, I don’t know, a zillion other files. And many of those files are generic containers, containing more files. And none of these files are named. Of course. It’s easy enough to notice that there are nine files per Pokémon, since the sizes follow a rough pattern like the sprites did in Diamond and Pearl. (You’d think that they’d use GARC’s two levels of nesting to group the per-Pokémon files together, but apparently not.)

At this point, I had zero experience with 3D — in fact, working on this was my introduction to 3D and Blender — so I didn’t get very far on my own. I basically had to wait a few years for other people to figure it out, look at their source code, replicate it myself, and then figure out some of the bits they missed. The one thing I did get myself was texture animations, which are generally used to make Pokémon change expressions — last I saw, no one had gotten those ripped, but I managed it. Hooray. I’m sure someone else has done the same by now.

Anyway, I bring up models because of two very weird things that I never would’ve guessed in a million years.

One was the mesh data itself. A mesh is just the description of a 3D model’s shape — its vertices (points), the edges between vertices, and the faces that fill in the space between the edges.

And, well, those are the three parts to a basic mesh. A few very simple model formats are even just those things written out: a list of vertices (defined by three numbers each, x y z), a list of edges (defined by the two vertices they connect), and a list of faces (defined by their edges).

It should be easy to find models by looking for long lists of triplets of numbers — vertex coordinates. Well, not quite. Pokémon models are stored as compiled shaders.

A shader is a simple kind of program that runs directly on a video card, since video cards tend to be a more appropriate place for doing a bunch of graphics-related math. On a desktop or phone or whatever, you’d usually write a shader as text, then compile it when your program/game runs. In fact, you have to do this, since the compilation is different for each kind of video card.

But Pokémon games only have to worry about one video card: the graphics chip in the 3DS. And there’s absolutely no reason to waste time compiling shaders while the game is running, when they could just do it ahead of time and put the compiled shader in the game directly. (Incidentally, the Dolphin emulator recently wrote about how GameCube games do much the same thing.)

So they did that. Thankfully, the compiled shader is much simpler than machine code, and the parts I care about are just the parts that load in the mesh data — which mostly looks like opcodes for “here’s some data”, followed by some data. It would probably be possible to figure out without knowing anything about the particular graphics chip, but if you didn’t know it was supposed to be a shader, you’d be mighty confused by all the mesh data surrounded by weird extra junk that doesn’t look at all like mesh data.

The other was skeletal animation. The basic idea is that you want to make a high-resolution model move around, but it would be a huge pain in the ass to describe the movement of every single vertex. Instead, you make an invisible “skeleton” — a branching tree of bones. The bones tend to follow major parts of the body, so they do look like very simple skeletons, with spines and arms and whatnot (though of course skeletons aren’t limited only to living creatures). Every vertex attaches to one or more of those bones — a rough first pass of this can be done automatically — and then by animating the much simpler skeleton, vertices will all move to match the bones they’re attached to.

The skeleton itself isn’t too surprising. It’s a tree, whatever; we’ve seen one of those already, with the DS directory structure. The skeletons and models are in a neutral pose by default: T for bipeds, simply standing on all fours for quadrupeds, etc. All of this is pretty straightforward.

But then there are the animations themselves.

An animation has some number of keyframes which specify a position, rotation, and size for each bone. Animating the skeleton involves smoothly moving each bone from one keyframe’s position to the next.

Position, rotation, and size each exist in three dimensions, so there are nine possible values for each keyframe. You might expect a set of nine values, then, times the number of keyframes, times the number of bones.

But no! These animations are stored the other way: each of those nine values is animated separately per bone. Also, each of those nine values can have a different number of keyframes, even for the same bone. Also, each of those nine values is optional, and if it’s not animated then its keyframes are simply missing, and there’s a set of bitflags indicating which values are present.

Okay, well, you might at least expect that a single value’s keyframes are given by a list of numbers, right?

Not quite! Such a set of keyframes has an initial “scale” and “offset”, given as single-precision floating point numbers (which are fairly accurate). Each keyframe then gives a “value” as an integer, which is actually the numerator of a fraction whose denominator is 65,535. So the actual value of each keyframe is:

Maybe this is a more common scheme than I suspect. Animation does take up an awful lot of space, and this isn’t an entirely unreasonable way to squish it down. The fraction thing is just incredibly goofy at first blush. I have no idea how anyone figured out what was going on there. (It’s used for texture animation, too.)

Anyway, thanks mostly to other people’s hard work, I managed to write a script that can dump models and then play them with a pretty decent in-browser model viewer. I never got around to finishing it, which is a shame, because it took so much effort and it’s so close to being really good. (My local copy has texture animation mostly working; the online version doesn’t yet.)

Hopefully I will someday, because I think this is pretty dang cool, and there’s a lot of interesting stuff that could be done with it. (For example, one request: applying one Pokémon’s animations to another Pokémon’s model. Hm.)

The one thing that really haunts me about it is the outline effect. It’s not actually the effect from the games; I had to approximate it, and there are a few obvious ways it falls flat. I would love to exactly emulate what the games do, but I just don’t know what that is. But maybe… maybe there’s a chance I can find the compiled shader and figure it out. Maybe. Somehow.

Some annoying edge cases

Let’s finish up with some small bumps in the road that are still fresh in my mind.

TMs are still in the Pokémon data, as is compatibility with move tutors. Alas, the lists of what the TMs and tutor moves are are embedded in the code, just like in the Game Boy days. You don’t really need to know the TM order, since they have a numbering exposed to the player in-game, and TM compatibility is in that same order… but move tutors have no natural ordering, so you have to either match them up by hand or somehow find the list in the binary.

I had a similar problem with incense items, which each affect the breeding outcome for a specific Pokémon. In Ruby and Sapphire, the incense effects were hardcoded. I don’t mean they were a data structure baked into the code; I mean they were actually “if the baby is this species and one parent is holding this incense, do this; otherwise,” etc. I spent a good few hours hunting for something similar in later games, to no avail — I’d searched for every permutation of machine code I could think of and come up with nothing. I was about to give up when someone pointed out to me that incense is now a data structure; it’s just in the one format I’d forgotten to try searching for. Alas.

Moves have a bunch of metadata, like “status effect inflicted” or “min/max number of turns to last”. Trouble is, I’m pretty sure that same information is duplicated within the code for each individual move — most moves get their own code, and there’s no single “generic move” function. Which raises the question… what is this metadata actually used for? Is it useful to expose on veekun? Is it guaranteed to be correct? I already know that some of it is a little misleading; for example, Tri Attack is listed as inflicting some mystery one-off status effect, because the format doesn’t allow expressing what it actually does (inflict one of burn, freezing, or paralysis at random).

Items have a similar problem: they get a bunch of their own data, but it’s not entirely clear what most of it is used for. It’s not even straightforward to identify how the game decides which items go in which pocket.

Moves also have flags, and it took some effort to figure out what each of them meant. Sun and Moon added a new flag, and I agonized over it for a while before I was fed the answer: it’s an obscure detail relating to move animations. No idea how anyone figured that out.

In Omega Ruby and Alpha Sapphire, there are two lists of item names. They’re exactly identical, with one exception: in Korean, the items “PP Up” and “PP Max” have their names written with English letters “PP” in one list but with Hangul in the other list. Why? No idea.

Evolution types are numbered. Method 4 is a regular level up; method 5 is a trade; method 21 is levelling up while knowing a specific move, which is given as a parameter. Cool. But there are two oddities. Karrablast and Shelmet only evolve when traded with each other, but the data doesn’t indicate this in any way; they both get the same unique evolution method, but there’s no parameter to indicate what they need to be traded with, as you might expect. Also, Shedinja isn’t listed as an evolution at all, since it’s produced as a side effect of Nincada’s evolution (which is listed as a normal level-up). To my considerable chagrin, that means neither of these cases can be ripped 100% automatically.

Pokémon are listed in a different order, depending on context. Sometimes they’re identified by species, e.g. Deoxys. Sometimes they’re identified by form, e.g. Attack Forme Deoxys. Sometimes they’re identified by species and also a separate per-species form number. Sometimes the numbering includes aesthetic-only forms, like Unown, that only affect visuals. But sprites and models both seem to have their own completely separate numberings, which are (of course) baked into the binary.

Incidentally, it turns out that all of the Totem Pokémon in Sun and Moon count as distinct forms! They’re just not obtainable. Do I expose them on veekun, then? I guess so?

Encounters are particularly thorny. The data is simple enough: for each map, there’s a list of Pokémon that can be encountered by various methods (e.g. walking in grass, fishing, surfing). But each of those Pokémon appears at a different rate, and those rates are somewhere in the code, not in the data. And there are some weird cases like swarms, which have special rules. And there are unique encounters that aren’t listed in this data at all, and which veekun has thus never had. And how do you even figure out where a map is anyway, when a named place can span multiple maps, and the encounters are only very slightly different in each map? (I’m told this has gotten a lot more data-oriented in Sun and Moon, but I haven’t dug into it yet myself.)

Anyway, that’s why veekun is taking so long. Also because I’ve spent several days not working on veekun so I could write this post, which could be much longer but has gone on more than long enough already. I hope some of this was interesting!

Oh, and all my recent code is on the pokedex GitHub. The model extraction stuff isn’t up yet, but it will be… eventually? Next time I work on it, maybe?