Anonymous asks:

something about how we tweak physics to “work” better in games?

Ho ho! Work. Get it? Like in physics…?

Hitboxes

“Hitbox” is perhaps not the most accurate term, since the shape used for colliding with the environment and the shape used for detecting damage might be totally different. They’re usually the same in simple platformers, though, and that’s what most of my games have been.

The hitbox is the biggest physics fudge by far, and it exists because of a single massive approximation that (most) games make: you’re controlling a single entity in the abstract, not a physical body in great detail.

That is: when you walk with your real-world meat shell, you perform a complex dance of putting one foot in front of the other, a motion you spent years perfecting. When you walk in a video game, you press a single “walk” button. Your avatar may play an animation that moves its legs back and forth, but since you’re not actually controlling the legs independently (and since simulating them is way harder), the game just treats you like a simple shape. Fairly often, this is a box, or something very box-like.

Since the player has no direct control over the exact placement of their limbs, it would be slightly frustrating to have them collide with the world. This is especially true in cases like the above, where the tail and left ear protrude significantly out from the main body. If that Eevee wanted to stand against a real-world wall, she would simply tilt her ear or tail out of the way, so there’s no reason for the ear to block her from standing against a game wall. To compensate for this, the ear and tail are left out of the collision box entirely and will simply jut into a wall if necessary — a goofy affordance that’s so common it doesn’t even register as unusual. As a bonus (assuming this same box is used for combat), she won’t take damage from projectiles that merely graze past an ear.

(One extra consideration for sprite games in particular: the hitbox ought to be horizontally symmetric around the sprite’s pivot — i.e. the point where the entity is truly considered to be standing — so that the hitbox doesn’t abruptly move when the entity turns around!)

Corners

Treating the player (and indeed most objects) as a box has one annoying side effect: boxes have corners. Corners can catch on other corners, even by a single pixel. Real-world bodies tend to be a bit rounder and squishier and this can tolerate grazing a corner; even real-world boxes will simply rotate a bit.

Ah, but in our faux physics world, we generally don’t want conscious actors (such as the player) to rotate, even with a realistic physics simulator! Real-world bodies are made of parts that will generally try to keep you upright, after all; you don’t tilt back and forth much.

One way to handle corners is to simply remove them from conscious actors. A hitbox doesn’t have to be a literal box, after all. A popular alternative — especially in Unity where it’s a standard asset — is the pill-shaped capsule, which has semicircles/hemispheres on the top and bottom and a cylindrical body in 3D. No corners, no problem.

Of course, that introduces a new problem: now the player can’t balance precariously on edges without their rounded bottom sliding them off. Alas.

If you’re stuck with corners, then, you may want to use a corner bump, a term I just made up. If the player would collide with a corner, but the collision is only by a few pixels, just nudge them to the side a bit and carry on.

When the corner is horizontal, this creates stairs! This is, more or less kinda, how steps work in Doom: when the player tries to cross from one sector into another, if the height difference is 24 units or less, the game simply bumps them upwards to the height of the new floor and lets them continue on.

Implementing this in a game without Doom’s notion of sectors is a little trickier. In fact, I still haven’t done it. Collision detection based on rejection gets it for free, kinda, but it’s not very deterministic and it breaks other things. But that’s a whole other post.

Gravity

Gravity is pretty easy. Everything accelerates downwards all the time. What’s interesting are the exceptions.

Jumping

Jumping is a giant hack.

Think about how actual jumping works: you tense your legs, which generally involves bending your knees first, and then spring upwards. In a platformer, you can just leap whenever you feel like it, which is nonsense. Also you go like twenty feet into the air?

Worse, most platformers allow variable-height jumping, where your jump is lower if you let go of the jump button while you’re in the air. Normally, one would expect to have to decide how much force to put into the jump beforehand.

But of course this is about convenience of controls: when jumping is your primary action, you want to be able to do it immediately, without any windup for how high you want to jump.

(And then there’s double jumping? Come on.)

Air control is a similar phenomenon: usually you’d jump in a particular direction by controlling how you push off the ground with your feet, but in a video game, you don’t have feet! You only have the box. The compromise is to let you control your horizontal movement to a limited degree in midair, even though that doesn’t make any sense. (It’s way more fun, though, and overall gives you more movement options, which are good to have in an interactive medium.)

Air control also exposes an obvious place that game physics collide with the realistic model of serious physics engines. I’ve mentioned this before, but: if you use Real Physics™ and air control yourself into a wall, you might find that you’ll simply stick to the wall until you let go of the movement buttons. Why? Remember, player movement acts as though an external force were pushing you around (and from the perspective of a Real™ physics engine, this is exactly how you’d implement it) — so air-controlling into a wall is equivalent to pushing a book against a wall with your hand, and the friction with the wall holds you in place. Oops.

Ground sticking

Another place game physics conflict with physics engines is with running to the top of a slope. On a real hill, of course, you land on top of the slope and are probably glad of it; slopes are hard to climb!

In a video game, you go flying. Because you’re a box. With momentum. So you hit the peak and keep going in the same direction. Which is diagonally upwards.

Projectiles

To make them more predictable, projectiles generally aren’t subject to gravity, at least as far as I’ve seen. The real world does not have such an exemption. The real world imposes gravity even on sniper rifles, which in a video game are often implemented as an instant trace unaffected by anything in the world because the bullet never actually exists in the world.

Resistance

Ah. Welcome to hell.

Water

Water is an interesting case, and offhand I don’t know the gritty details of how games implement it. In the real world, water applies a resistant drag force to movement — and that force is proportional to the square of velocity, which I’d completely forgotten until right now. I am almost positive that no game handles that correctly. But then, in real-world water, you can push against the water itself for movement, and games don’t simulate that either. What’s the rough equivalent?

The Sonic Physics Guide suggests that Sonic handles it by basically halving everything: acceleration, max speed, friction, etc. When Sonic enters water, his speed is cut; when Sonic exits water, his speed is increased.

That last bit feels validating — I could swear Metroid Prime did the same thing, and built my own solution around it, but couldn’t remember for sure. It makes no sense, of course, for a jump to become faster just because you happened to break the surface of the water, but it feels fantastic.

The thing I did was similar, except that I didn’t want to add a multiplier in a dozen places when you happen to be underwater (and remember which ones need it to be squared, etc.). So instead, I calculate everything completely as normal, so velocity is exactly the same as it would be on dry land — but the distance you would move gets halved. The effect seems to be pretty similar to most platformers with water, at least as far as I can tell. It hasn’t shown up in a published game and I only added this fairly recently, so I might be overlooking some reason this is a bad idea.

(One reason that comes to mind is that velocity is now a little white lie while underwater, so anything relying on velocity for interesting effects might be thrown off. Or maybe that’s correct, because velocity thresholds should be halved underwater too? Hm!)

Notably, air is also a fluid, so it should behave the same way (just with different constants). I definitely don’t think any games apply air drag that’s proportional to the square of velocity.

Friction

Friction is, in my experience, a little handwaved. Probably because real-world friction is so darn complicated.

Consider that in the real world, we want very high friction on the surfaces we walk on — shoes and tires are explicitly designed to increase it, even. We move by bracing a back foot against the ground and using that to push ourselves forward, so we want the ground to resist our push as much as possible.

In a game world, we are a box. We move by being pushed by some invisible outside force, so if the friction between ourselves and the ground is too high, we won’t be able to move at all! That’s complete nonsense physically, but it turns out to be handy in some cases — for example, highish friction can simulate walking through deep mud, which should be difficult due to fluid drag and low friction.

But the best-known example of the fakeness of game friction is video game ice. Walking on real-world ice is difficult because the low friction means low grip; your feet are likely to slip out from under you, and you’ll simply fall down and have trouble moving at all. In a video game, you can’t fall down, so you have the opposite experience: you spend most of your time sliding around uncontrollably. Yet ice is so common in video games (and perhaps so uncommon in places I’ve lived) that I, at least, had never really thought about this disparity until an hour or so ago.

Game friction vs real-world friction

Real-world friction is a force. It’s the normal force (which is the force exerted by the object on the surface) times some constant that depends on how the two materials interact.

Force is mass times acceleration, and platformers often ignore mass, so friction ought to be an acceleration — applied against the object’s movement, but never enough to push it backwards.

I haven’t made any games where variable friction plays a significant role, but my gut instinct is that low friction should mean the player accelerates more slowly but has a higher max speed, and high friction should mean the opposite. I see from my own source code that I didn’t even do what I just said, so let’s defer to some better-made and well-documented games: Sonic and Doom.

In Sonic, friction is a fixed value subtracted from the player’s velocity (regardless of direction) each tic. Sonic has a fixed framerate, so the units are really pixels per tic squared (i.e. acceleration), multiplied by an implicit 1 tic per tic. So far, so good.

But Sonic’s friction only applies if the player isn’t pressing ← or →. Hang on, that isn’t friction at all; that’s just deceleration! That’s equivalent to jogging to a stop. If friction were lower, Sonic would take longer to stop, but otherwise this is only tangentially related to friction.

(In fairness, this approach would decently emulate friction for non-conscious sliding objects, which are never going to be pressing movement buttons. Also, we don’t have the Sonic source code, and the name “friction” is a fan invention; the Sonic Physics Guide already uses “deceleration” to describe the player’s acceleration when turning around.)

Okay, let’s try Doom. In Doom, the default friction is 90.625%.

Hang on, what?

Yes, in Doom, friction is a multiplier applied every tic. Doom runs at 35 tics per second, so this is a multiplier of 0.032 per second. Yikes!

This isn’t anything remotely like real friction, but it’s much easier to implement. With friction as acceleration, the game has to know both the direction of movement (so it can apply friction in the opposite direction) and the magnitude (so it doesn’t overshoot and launch the object in the other direction). That means taking a semi-costly square root and also writing extra code to cap the amount of friction. With a multiplier, neither is necessary; just multiply the whole velocity vector and you’re done.

There are some downsides. One is that objects will never actually stop, since multiplying by 3% repeatedly will never produce a result of zero — though eventually the speed will become small enough to either slip below a “minimum speed” threshold or simply no longer fit in a float representation. Another is that the units are fairly meaningless: with Doom’s default friction of 90.625%, about how long does it take for the player to stop? I have no idea, partly because “stop” is ambiguous here! If friction were an acceleration, I could divide it into the player’s max speed to get a time.

All that aside, what are the actual effects of changing Doom’s friction? What an excellent question that’s surprisingly tricky to answer. (Note that friction can’t be changed in original Doom, only in the Boom port and its derivatives.) Here’s what I’ve pieced together.

Doom’s “friction” is really two values. “Friction” itself is a multiplier applied to moving objects on every tic, but there’s also a move factor which defaults to \(\frac{1}{32} = 0.03125\) and is derived from friction for custom values.

Every tic, the player’s velocity is multiplied by friction, and then increased by their speed times the move factor.

Eventually, the reduction from friction will balance out the speed boost. That happens when \(v(n) = v(n - 1)\), so we can rearrange it to find the player’s effective max speed:

For vanilla Doom’s move factor of 0.03125 and friction of 0.90625, that becomes:

Curiously, “speed” is three times the maximum speed an actor can actually move. Doomguy’s run speed is 50, so in practice he moves a third of that, or 16⅔ units per tic. (Of course, this isn’t counting SR40, a bug that lets Doomguy run ~40% faster than intended diagonally.)

So now, what if you change friction? Even more curiously, the move factor is calculated completely differently depending on whether friction is higher or lower than the default Doom amount:

That’s pretty weird? Complicating things further is that low friction (which means muddy terrain, remember) has an extra multiplier on its move factor, depending on how fast you’re already going — the idea is apparently that you have a hard time getting going, but it gets easier as you find your footing. The extra multiplier maxes out at 8, which makes the two halves of that function meet at the vanilla Doom value.

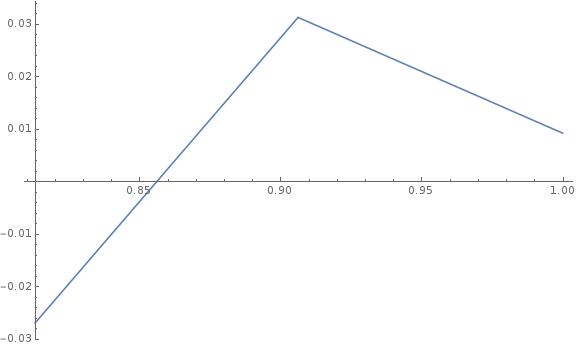
That very top point corresponds to the move factor from the original game. So no matter what you do to friction, the move factor becomes lower. At 0.85 and change, you can no longer move at all; below that, you move backwards.

From the formula above, it’s easy to see what changes to friction and move factor will do to Doomguy’s stable velocity. Move factor is in the numerator, so increasing it will increase stable velocity — but it can’t increase, so stable velocity can only ever decrease. Friction is in the denominator, but it’s subtracted from 1, so increasing friction will make the denominator a smaller value less than 1, i.e. increase stable velocity. Combined, we get this relationship between friction and stable velocity.

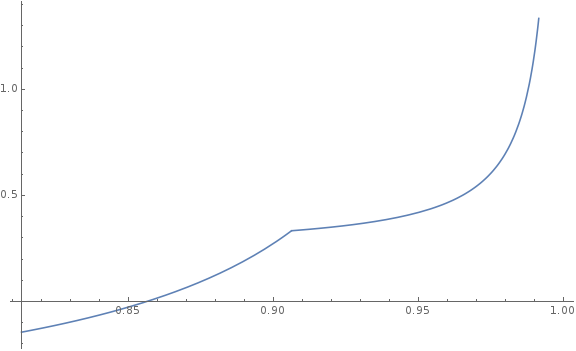
As friction approaches 1, stable velocity grows without bound. This makes sense, given the definition of \(v(n)\) — if friction is 1, the velocity from the previous tic isn’t reduced at all, so we just keep accelerating freely.

All of this is why I’m wary of using multipliers.

Anyway, this leaves me with one last question about the effects of Doom’s friction: how long does it take to reach stable velocity? Barring precision errors, we’ll never truly reach stable velocity, but let’s say within 5%. First we need a closed formula for the velocity after some number of tics. This is a simple recurrence relation, and you can write a few terms out yourself if you want to be sure this is right.

Our initial velocity is zero, so the first term disappears. Set this equal to the stable formula and solve for n:

“Speed” and move factor disappear entirely, which makes sense, and this is purely a function of friction (and how close we want to get). For vanilla Doom, that comes out to 30.4, which is a little less than a second. For other values of friction:

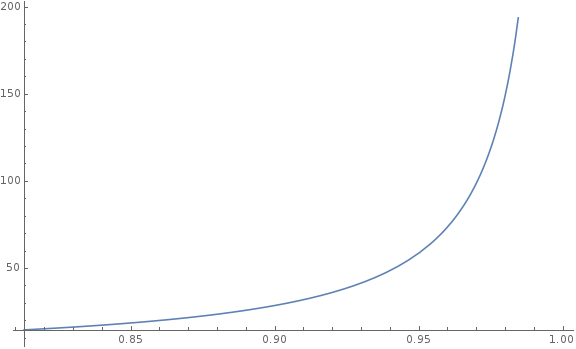
As friction increases (which in Doom terms means the surface is more slippery), it takes longer and longer to reach stable speed, which is in turn greater and greater. For lesser friction (i.e. mud), stable speed is lower, but reached fairly quickly. (Of course, the extra “getting going” multiplier while in mud adds some extra time here, but including that in the graph is a bit more complicated.)

I think this matches with my instincts above. How fascinating!

What’s that? This is way too much math and you hate it? Then don’t use multipliers in game physics.

Uh

That was a hell of a diversion!

I guess the goofiest stuff in basic game physics is really just about mapping player controls to in-game actions like jumping and deceleration; the rest consists of hacks to compensate for representing everything as a box.